Je kent het wel: je ziet een raadsel dat op het eerste gezicht zo basaal lijkt dat je denkt: "Dit kan ik makkelijk oplossen." Maar dan begin je met rekenen en plotseling zit je vast in een wiskundige modderpoel. Veel volwassenen komen hierop vast te zitten, vaak omdat de context mist die ze op de middelbare school kregen.
Dit specifieke meetkundige probleem, dat scholieren in Australië soms voorgeschoteld krijgen, lijkt een eenvoudige oppervlakteberekening. Maar de truc zit hem in één cruciaal detail over de getallen die je mag gebruiken. Als je hier te snel doorheen gaat, mis je de sleutel.
De schijnbaar onschuldige vorm
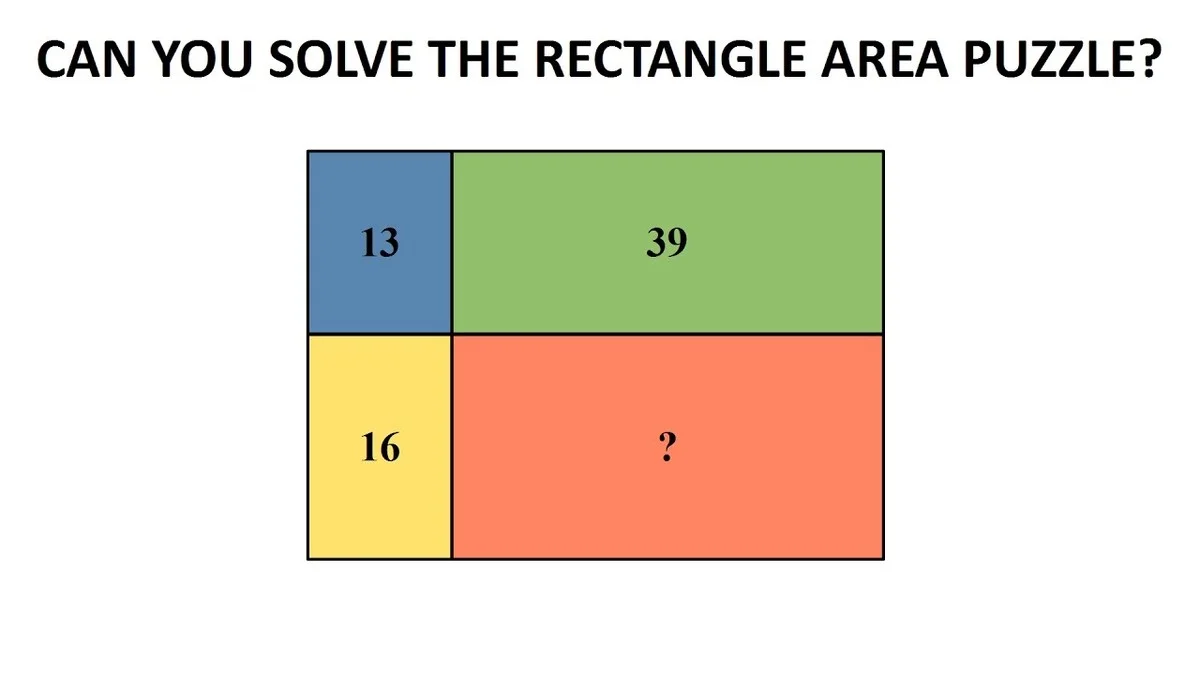
Voor ons ligt een rechthoek die verdeeld is in vier kleinere rechthoeken. We krijgen de totale som van de gebieden die door de variabelen a, b, c en d worden vertegenwoordigd. De som a + b + c + d = 63. Bovenal is bekend dat a, b, c, en d gehele getallen moeten zijn.
De kernvraag is: Wat is de maximaal mogelijke oppervlakte van het oranje gekleurde gebied? Dit gebied bestaat uit de delen ab + bc + cd. Verwar dit niet met het totale oppervlak. Dit is waar de meeste mensen de fout in gaan.
De valkuil van de intuïtie
Wanneer ik dit soort opgaven zie, merk ik dat mensen direct proberen a, b, c en d te verdelen alsof het allemaal min of meer gelijke delen moeten zijn. Dat is de aanname die je moet vermijden. Je moet de formule herschrijven om te zien waar de maximale waarde vandaan komt.
De slimme stap is om de formule te herschikken naar:
- (a + c)(b + d) – ad
Dat ziet er al beter uit, maar het verbergt nog steeds de oplossing. Het is vergelijkbaar met hoe je in Nederland je belastingaangifte invult; je zoekt altijd naar de aftrekposten die de grootste impact hebben.
De rol van de randvoorwaarden
Om de oranje oppervlakte zo groot mogelijk te maken, moeten we de term die we aftrekken zo klein mogelijk maken. Dat betekent dat we ad zo klein mogelijk moeten maken.
Aangezien a en d gehele getallen moeten zijn, is de kleinst mogelijke waarde die ze kunnen aannemen: 1. Dit is de échte 'insider tip' die het hele probleem oplost. Als a = 1 en d = 1, dan moet b + c = 61.
De kwadratische sprong
Nu de som b + c vastligt, moeten we het resterende deel maximaliseren. De uitdrukking wordt dan: Max (1 + c)(62 – c) – 1. Dit levert uiteindelijk een kwadratische uitdrukking op waarin c de onbekende is.
Wiskundig gezien ligt het maximum van een parabool op het punt x = -β/2α. In ons geval is dat c = 30,5. Grote kans dat je nu baalt. Want c moet een geheel getal zijn!
Dit is de punt waarop je even moet pauzeren. Omdat de top niet precies op een geheel getal ligt, weet je dat de maximale waarde bereikt wordt als je kiest voor de dichtstbijzijnde gehele getallen. Dus c = 30 óf c = 31.
Of je nu 30 of 31 kiest voor c (en dus 31 of 30 voor b), de uitkomst is hetzelfde: De maximaal mogelijke oppervlakte is 991.
Wat dit je leert over alledaagse problemen
Dit is meer dan een wiskundeklus; het is een les in optimalisatie. Net als wanneer je probeert de kortste route naar de Ikea te vinden in de spits in Utrecht, moet je soms de meest voor de hand liggende indeling van de vlakken negeren en focussen op het minimaliseren van de 'verliesposten'.
Heb je deze opgave meteen ook opgelost, of moest je net als ik de getallen eerst op 1 zetten? Laat het weten in de reacties!