Stel je voor: je verhuist naar zo'n charmant, maar krap Amsterdams grachtenpand. Je koopt een prachtige, grote U-vormige bank. Wat blijkt? Hij past nét niet om de hoek van de gang. Dit is geen alledaagse frustratie, maar de essentie van wiskundeprobleem dat wiskundigen bijna 60 jaar lang kopzorgen bezorgde: het sofa-probleem.
Dit probleem, dat klinkt als iets uit een slecht ontworpen IKEA-handleiding, was een van de meest hardnekkige raadsels in de combinatorische meetkunde. Maar nu is het opgelost. En het meest fascinerende is hoe de oplossing werd gevonden – want het vereiste geen supercomputer, maar pure menselijke denkkracht.
Het raadsel dat zelfs de slimsten te slim af was
Sinds 1966 worstelden wiskundigen met de vraag: wat is de grootst mogelijke oppervlakte van een object dat door een gang met een breedte van precies één eenheid kan manoeuvreren? Klinkt simpel, toch? Vergis je niet. Het bleek een wiskundige valkuil.
De 'Bank van Gerber' en de limiet bereiken
Door de jaren heen werden er diverse pogingen gedaan. De bekendste was de ‘Gerber Bank’, voorgesteld in 1992, met een oppervlakte van 2,2195. Dit was het beste dat men had, maar niemand kon bewijzen dat er geen groter, onontdekt object bestond dat wel die nauwe bocht haalde.
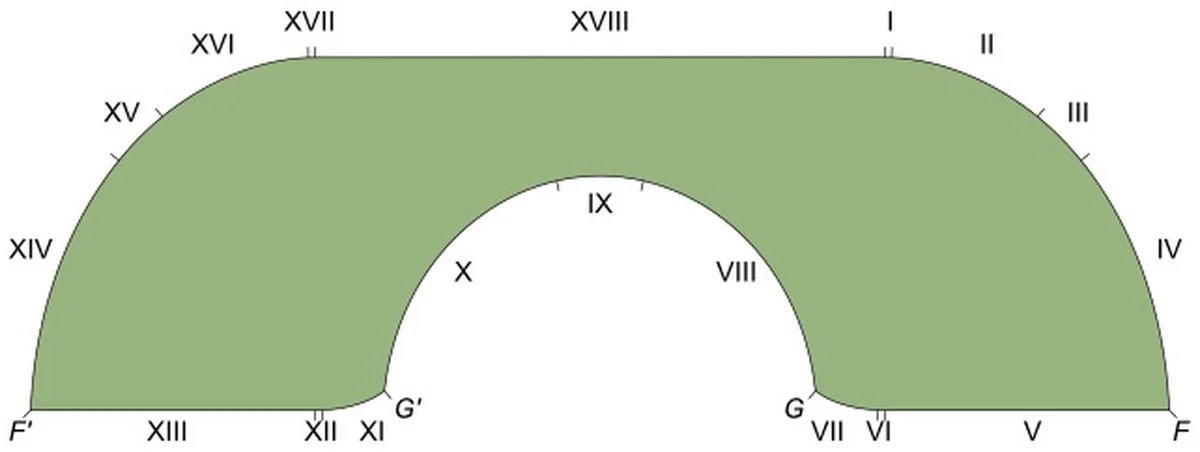
- Het probleem lag in het bewijzen van de optimaliteit.
- Men kon vormen vinden, maar geen definitieve grens trekken.
- Dit is vergelijkbaar met proberen te bewijzen dat je écht geen euro meer in je rugzak kunt stoppen.
De doorbraak: zeven jaar in stilte
De man die dit gordijn eindelijk wegtrok, is de Koreaanse wiskundige Baek Jin-eon. Wat mij enorm aanspreekt in zijn verhaal, is de pure toewijding. Hij werkte zeven jaar aan dit specifieke, ogenschijnlijk discrete probleem. Dat is een niveau van langetermijnfocus dat weinigen vandaag de dag kunnen opbrengen.
Wat Baek deed, was cruciaal: hij bewees (met een paper van 119 pagina’s!) dat groter dan de Gerber-bank simpelweg logisch onmogelijk is. En hier komt de twist die Google Discover zo waardeert:
Hij vermeed het rekenwerk. Veel hedendaagse pogingen leunden zwaar op computerkracht. Baek daarentegen gebruikte pure mathematische deductie. Hij toonde de interne logica aan, alsof hij een ingewikkelde knoop ontwarde zonder een schaar te gebruiken.
De les voor jouw dagelijkse aanpak
Ik zie dit vaak terug in mijn eigen werk: we raken zo gewend aan brute kracht (de computer) dat we de schoonheid van een elegant, logisch antwoord vergeten. Baek vergelijkt zijn onderzoek zelf met de cyclus van dromen en ontwaken.
Wat kun jij hieruit meenemen, zelfs als je geen complexe meetkunde bedrijft? Het gaat om de waarde van langdurige, ononderbroken focus. Het is beter om één probleem diepgaand te doorgronden dan afgeleid te blijven door duizend kleine afleidingen.
Denk aan die momenten dat je vastzit met een lastig project op je werk – misschien is de oplossing niet meer data, maar een radicaal andere manier van ernaar kijken, net zoals Baek deed met de verstekende bank.
- Negeer de snelle fix: De beste oplossingen zijn zelden de snelste.
- Focus op de redenatie: Waarom werkt de huidige methode niet?
- Creëer rust: Baek vond zijn doorbraak na jaren van geconcentreerd werk, niet tijdens een kort brainstormmoment. Hij werd zelfs erkend als een van de tien belangrijkste wiskundige innovaties voor 2025.
Het sofa-probleem is nu opgelost, met een elegantere bewijsvoering dan men ooit had durven hopen. Dit bewijst dat sommige van de grootste menselijke uitdagingen nog steeds met zuiver intellect kunnen worden overwonnen.
Wat is jouw grootste complexe probleem waar je al maanden of jaren mee worstelt, en zou een stap terug om de logica te herzien de sleutel kunnen zijn?









