We kennen allemaal die momenten waarop een schijnbaar onoplosbaar probleem plotseling helder wordt. Maar wat als die ‘aha’-ervaring niet alleen jouw dag, maar de hele internationale wiskundegemeenschap beïnvloedt? Een docent uit Focșani deed exact dit, geïnspireerd door een opmerking van de huidige president van Roemenië.
Het gaat om een wiskundeprobleem dat zo berucht was dat slechts 11 mensen ter wereld het ooit bij de Internationale Wiskunde Olympiade in 1988 kraakten. Nu, jaren later, heeft een leraar deze specifieke puzzel omgetoverd tot een algemene, elegante formule. Als jij ooit vastloopt op een complex cijferwerk, is dit verhaal relevant voor je.
De legendarische opgave uit Australië
De Olympiade van 1988 staat bekend om een van de zwaarste opgaven in zijn geschiedenis: een typisch voorbeeld van een specifiek geval dat complexe berekeningen vergde. Onder degenen die de opgave wisten te kraken, bevond zich een jonge Nicușor Dan, nu president van het land.
Het probleem was ontworpen om slechts één specifieke oplossing te belonen. Het was geen formule; het was een bijna ambachtelijke manier van puzzelen. Veel mensen, inclusief ikzelf bij het bestuderen van oude Olympiades, zien dit als een unieke prestatie, maar niet als iets dat je kunt generaliseren.
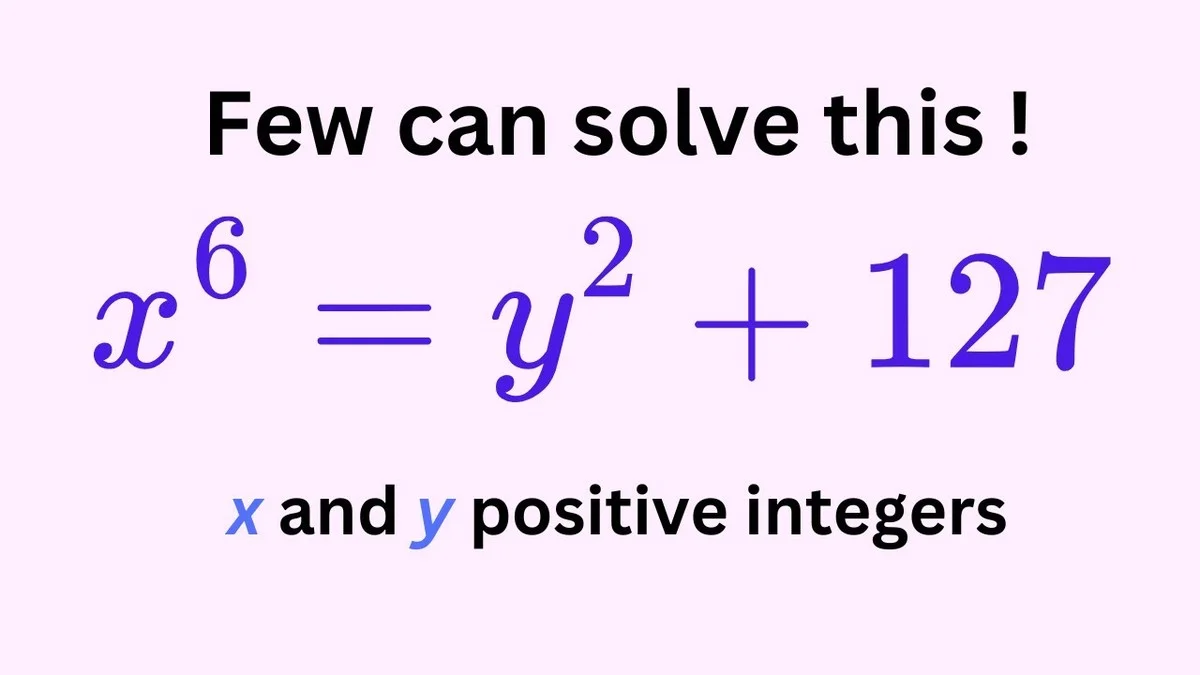
De onverwachte vonk: Een tv-interview
Professor Mihai Teodor uit Focșani zag president Dan recent in een interview vertellen hoe hij destijds te werk ging. Dan omschreef hoe hij anderhalf uur nodig had en vijf pagina’s volschreef om tot die ene oplossing te komen.
Dit was het cruciale punt. Teodor dacht: "Als het voor dit ene geval werkt, kán er dan geen universele structuur achter zitten?"
Hij zag een specifieke truc, maar zocht de wetmatigheid erachter, alsof je leert hoe een complexe Bosch-vaatwasser werkt, en dan een handleiding schrijft voor déze machine, maar uiteindelijk een methode vindt voor álle vaatwassers van dat merk.
De sprong van ‘geval’ naar ‘theorie’
In jouw dagelijkse werk, of het nu gaat om het oplossen van Excel-fouten of het optimaliseren van een lokale bedrijfslogistiek, loop je vaak tegen dergelijke specifieke hindernissen aan. Teodor deed precies dat, maar dan op universitair niveau.

Hij weigerde genoegen te nemen met het feit dat er slechts particuliere oplossingen met behulp van computers te vinden waren. Hij zocht de algemene formule. Hij wilde weten hoe de parameters a en b zich gedragen in alle mogelijke combinaties.
- Na intensief onderzoek identificeerde hij de wiskundige architectuur achter de opgave.
- Hij slaagde erin een formule te creëren die elke mogelijke oplossing beschrijft.
- Het probleem van 1988 is nu slechts nog een voetnoot, een simpel voorbeeld van zijn veel grotere theorie.
Publicatie in de ‘Wiskunde Bijbel’
Het resultaat van Teodor’s werk was zo significant dat het wereldwijd erkend werd. Zijn algemene demonstratie is gepubliceerd in de On-line Encyclopedia of Integer Sequences (OEIS). Dit is geen toevallige blog; het is een van de meest gerespecteerde wetenschappelijke databases ter wereld. Denk aan de OEIS als de Wikipedia voor wiskundige reeksen, maar dan met een veel strengere review-procedure.
Wat betekent dit praktisch voor ons? Deze generalisatie maakt het makkelijker om vergelijkbare vergelijkingen met gehele getallen op te lossen, iets wat studenten tot op de middelbare school bezighoudt. Heldere, snellere oplossingen zijn het directe gevolg.
Het is inspirerend: iemand zag hoe de huidige president van Roemenië een uitdaging overwon, en slaagde er vervolgens in om dat hele probleem te overstijgen en te verbeteren. Wat is volgens jou de meest over het hoofd geziene basiswet in jouw vakgebied die wacht om geverifieerd of gegeneraliseerd te worden?









